بر مرز مبهم جهان و هندسه: بازخوانی میراث میرزاخانی

سه‌شنبه، ۱۲ اوت ۲۰۱۴ (مصادف با ۲۱ مرداد ۹۳)، اعلام نام مریم میرزاخانی به‌ عنوان نخستین زن برنده مدال فیلدز در جهان، از این ریاضیدان ۳۷ ساله دانشگاه استنفورد، چهره‌ای‌ نام‌آشنا در رسانه‌های ایران و جهان ساخت. اما حال، اعلام خبر درگذشت ناگهانی این چهره ریاضیات محض، هم‌وطنان او و علاقه‌مندان به این رشته را به همان اندازه در بهت و تأثر فروبرده است. نظر به آنکه فراوان از سوابق تحصیلی و افتخارات میرزاخانی نوشته شده است، در ادامه مختصری را از برجسته‌ترین دستاورد او که در جهان ریاضیات به یادگار مانده، می‌خوانید؛ دستاوردی که گرچه در نمای نزدیک، انتزاعی و سخت‌فهم می‌نماید، اما در نمای باز، دستاوردی است در ردیف میراث نامداران تاریخ علم.

برجسته‌ترین دستاورد میرزاخانی در کسوت یک ریاضیدان، به مقاله ۱۷۲صفحه‌ای او در سال ۲۰۱۲ بازمی‌گردد که پس از نُه سال کار مداوم، آن را به اتفاق الکس اسکین، از ریاضیدانان دانش شیکاگو منتشر کرد. میرزاخانی در این مقاله موفق شد پاسخی را که استاد راهنمای تز دکتری‌اش کورتیس مک‌مولن به یک معمای دیرینه ریاضی داده بود، به طریقی کارآمد بسط بدهد.

به طور خلاصه، معمایی که مک‌مولن موفق به حل آن شد، به الگوی انحنای سطوح هذلولی ِ دوحفره‌ای مربوط می‌شد؛ و میرزاخانی موفق شده بود این پاسخ را به سطوح هذلولی n-حفره‌ای بسط بدهد. اما درک اهمیت چنین دستاوردی، به زبان فیزیک ملموس‌تر است.

پلی انتزاعی به سمت یک فیزیک «واقعی»تر

در فیزیک کلاسیک، «فضا» به منزله یک سطح تخت قلمداد می‌شود که اجسام بر روی آن واقع شده‌اند؛ و نیروی جاذبه نیز به منزله نیرویی دوربرد که این اجسام را به سمت یکدیگر جذب می‌کند. اما به مجرد طرح تئوری نسبیت عام اینشتین در سال ۱۹۱۶، جاذبه دیگر نه به عنوان یک نیرو، بلکه به عنوان «انحنای» فضا بازتعریف شد. در این تعریف جدید، فضا را تنها زمانی می‌توان «تخت» شمرد که در آن هیچ میدان جاذبه‌ای حضور نداشته باشد؛ و این در عمل ناممکن است، چراکه دست‌کم فرد ناظر در آن فضا حضور دارد.

لذا «فضا»ی نسبیتی ذاتاً ماهیتی غیرتخت دارد، و این را می‌‌توان از رفتار نور در اطراف اجسام پرجرم متوجه شد: نور همواره از نزدیک‌ترین خط بین مبدأ و مقصد می‌گذرد، و این در حالی‌ است که پرتوهای نور عبوری از کنار جسم سنگینی همچون خورشید، دچار «انحناء» می‌شوند. این انحناء به آن معنا نیست که پرتوهای نور از مسیر اصلی‌شان منحرف شده‌اند، بلکه بدین‌معناست که «فضا»ی پیرامون خورشید دچار انحناست: پرتوها همچنان از نزدیک‌ترین خط بین مبدأ و مقصد می‌گذرند، اما این بار در یک فضای منحنی. در ریاضیات، کوتاه‌ترین خط واصل دو نقطه اصطلاحاً «خط ژئودزیک» نامیده می‌شود؛ و در فیزیک، مسیر جابجایی نور عینی‌ترین مصداق یک خط ژئودزیک محسوب می‌شود.

اگرچه نسبیت عام تصویری واقع‌گرایانه‌تر از ساز و کار نیروی جاذبه عرضه می‌کند، اما در واقعیت امر، درک الگوی انحنای فضا، به‌ دلیل پیچیدگی توزیع جرم در یک سیستم فیزیکی واقعی، کاری بسیار دشوار است. حتی پیش از تدوین تئوری نسبیت عام نیز آیزاک نیوتن در کتاب دوران‌ساز «مبانی ریاضیاتی فلسفه طبیعی» (یا به اختصار، «پرینسیپیا»)، بر همین مبنا، دشواری مسأله تبیین دقیق حرکت ماه در سیستم سه‌گانه ماه-زمین-خورشید را مطرح کرده بود.

این مسأله در نیمه دوم قرن هجدهم، به بحث داغی بین ریاضیدانان و فیزیکدانان دوران بدل شد. ژان دالامبر و الکسی کلرو، دو ریاضیدانان و اخترشناس سرشناس فرانسوی، کوشیدند از طریق معادلات دیفرانسیل و ارتقای تقریب‌ها، به پاسخی برای این مسأله – که هم‌اینک به «مسأله سه‌جسم» مشهور شده بود – دست یابند. اما عاقبت در اواخر قرن نوزدهم بود که ریاضیدان آلمانی، ارنست برونز، و ریاضیدان فرانسوی آنری پوآنکاره، نشان دادند که ارائه یک راه حل کلی برای مسأله سه‌جسم، از طریق راهبردهای جبری میسر نخواهد بود؛ چراکه الگوی توزیع جاذبه در یک سیستم سه‌گانه، با هر بار صورت‌بندی مجدد مسأله، صورتی دیگر به خود می‌گیرد (به عبارت دقیق‌تر، سیستم‌های متشکل از سه جسم، «سیستم‌های دینامیکی» محسوب می‌شوند).

از طرفی در آن مقطع، ریاضیدان آلمانی، برنارد ریمان همزمان زمینه را برای عبور ریاضیات از سد هندسه اقلیدسی فراهم ساخته بود؛ اقدامی که سرانجام در چارچوب تئوری نسبیت عام صورتی فیزیکی به خود گرفت.

اما توصیف نسبیتی الگوی توزیع جاذبه در سیستم‌های دینامیکی، همچنان مستلزم تعیین الگوی انحنای فضا در این سیستم‌ها، یا به عبارت بهتر، تعیین کلیه خطوط ژئودزیک ممکنی بود که می‌توان بر فضای مدنظر متصور بود. درک الگوی انحنای فضا در چنین سیستم‌هایی که مدام تغییر حالت می‌دهند، خود مستلزم درک هندسه سطوح هذلولی (یعنی سطوحی با انحنای منفی، نظیر سطح یک زین اسب) است.

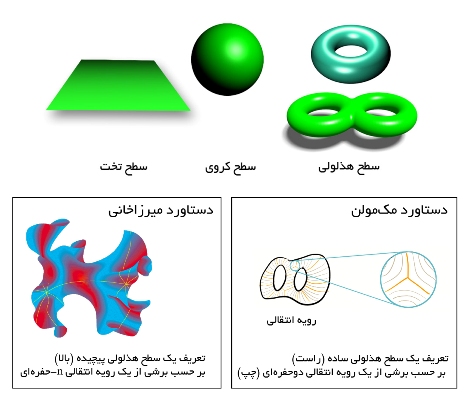
یک سطح هذلولی ساده را می‌توان به صورت برشی از یک رویه دونات‌مانندِ دو حفره‌ای (مانند سطح بیرونی محل تقاطع دو تایر به‌هم‌چسبیده) تصور کرد؛ اما برای درک الگوی انحنای سطوح هذلولی پیچیده‌تر باید عکس مسأله را پی گرفت: چنانچه سطح مدنظر را برشی از یک رویه وسیع‌تر تلقی کنیم، می‌توان پرسید که این رویه‌ی مفروض (که در اصطلاح ریاضی، «رویه انتقالی» نامیده می‌شود) از ادغام چند رویه ساده دونات‌‌مانند حاصل شده است؟ از آنجاکه هر رویه دونات‌‌مانندِ ساده از یک حفره‌ی میانی میزبانی می‌کند (کمااینکه هر تایر اتومبیل، از یک حفره‌ی میانی میزبانی می‌کند)، می‌توان الگوی انحنای سطوح هذلولی پیچیده را بر حسب تابعی از تعداد حفره‌های‌ رویه‌ انتقالی‌شان تعریف کرد.

مک‌مولن، استاد راهنمای پایان‌نامه دکتری میرزاخانی در دانشگاه هاروارد، در سال ۲۰۰۳ موفق شده بود الگوی انحنای یک رویه‌ انتقالی دوحفره‌ای را با تعیین کل خطوط ژئودزیک ممکن آن تبیین کند. اما میرزاخانی موفق شد همین رهیافت را برای رویه‌های انتقالی پیچیده‌تری با n حفره به ثمر برساند؛ اقدامی که فقط یک سال بعد، معتبرترین مدال دنیای ریاضی را برای وی به ارمغان آورد.

میرزاخانی به طریق بالقوه موفق شد چارچوبی را برای توصیف الگوی تطور انحنای فضا در یک سیستم دینامیکی (اعم از سیستم‌های فیزیکی متشکل از n جسم) تعریف کند؛ پرسشی که نخستین صورت‌بندی آن را ایزاک نیوتن، بنیان‌گذار فیزیک کلاسیک به ثمر رساند، و آلبرت اینشتین، از بنیان‌گذاران فیزیک جدید، آن را به زبان هندسه نااقلیدسی ترجمه کرد. از این نقطه‌نظر، اقدام میرزاخانی، یک زیرسازی هندسی برای احداث پلی انتزاعی است که در آینده می‌تواند ما را به سمت یک فیزیک انضمامی‌تر سوق بدهد؛ فیزیکی که در چارچوب آن می‌توان متغیرهای فیزیک کلاسیک را در پرتو رهیافت‌های فیزیک نسبیتی به یکدیگر مرتبط ساخت. هرچند که امروزه با به حاشیه رفتن توصیفات فیزیک کلاسیک از واقعیت، اهمیت این نوع ِ بالقوه از فیزیکْ یکسره تحت‌الشعاع توصیفات نسبیتی قرار گرفته و نیازی به تدوین آن احساس نمی‌شود، اما مسلماً تداوم تلاش‌های ریاضیدانی همچون میرزاخانی می‌توانست از مناسبات پیچیده بین نظریه و واقعیت، بیشتر پرده برگیرد.

نزد فیزیکدانان، جهان همیشه جایی پیچیده‌تر از تصورات‌شان بوده است. اما در جهانِ پس از ریاضیدانی همچون میرزاخانی، به خوبی می‌فهمیم که جهان چقدر از تصورات‌مان پیچیده‌تر است.

در همین زمینه:

یک ذهن زیبا: مریم میرزاخانی